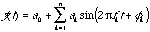
A spectre is haunting Europe …
-- Karl Marx and Friedrich Engels (1848)
During the Renaissance, when people looked through prisms at each other, they saw what appeared to be ghosts or spectra, multicolored and transparent images floating mysteriously near each other. What they were seeing, of course, were the colors of the image separating due to optical dispersion of the glass. The first scientific use of this phenomena was made by Newton, whose own theory of spectra turned out to be one of the few mistakes he published in physics. The true explanation was to wait for the contributions of W. H. Wollaston and J. Fraunhofer in the early 1800s, who based their results on the assumption that light was a wave, not a particle. (We now know it is both – but Newton was still wrong.) They improved their experiments by using a slit instead of a pinhole to collimate their light. This produced a line rather than a spot, and as a legacy we still refer to spectral lines, even when the data are handled digitally, and the frequency structure shown as a peak in a graph rather than as a brightly colored line on a white sheet. A group of spectral peaks is still called a "band," which is what a group of adjacent lines looked like. The band-width was the width in the optical spectrum of a group of lines; we still use this term today (without the hyphen) to denote the range of frequencies covered by a system.
Today, spectral analysis refers to any process that accounts for data as a sum of individual oscillations. When a musician listens to a chord played on a piano, and then goes to the piano and duplicates it, he has successfully performed spectral analysis. He has taken a complex sound and recognized it as a sum of individual oscillations. This is done using the hair cells of the inner ear, which are separated in the cochlear duct by their frequency sensitivity. That is what spectral analysis is – separation of a signal into different frequency components. The concept is made more complicated by the fact that every sound, even the roar of a waterfall, can be constructed from pure tones, although it takes a lot of them. But it is easier to reproduce the sound of a waterfall by recreating the amplitude of the sound as a function of time. This is called working in the "time domain." On the other hand, when we analyze a signal by breaking it up into a sum of pure frequencies, we say we are working in the "frequency domain."
Paleoclimate signals usually consist of a superposition of a few pure frequencies (also called lines, or tones) and background. Some of the analysis is best done in the time domain. This includes the precise timing of the glacial terminations, and the history of ice-rafting phenomena known as Heinrich events. A sudden event in the time domain, when described in the frequency domain, appears spread out over many frequencies, so it is difficult to study that way. Likewise, a single peak appearing in the frequency domain (e.g. at 41 kyr), appears as a relatively complex object in the time domain: a sinusoidal variation that covers all time. Spectral analysis and time domain analysis are best done together, since certain phenomena stand out in one representation, and other in the other. Non-periodic events are just as interesting as periodic ones; after all, it was a single dramatic event that appears to have killed the dinosaurs. But the frequency domain is extremely useful for many other astronomical forces (such as insolation) because astronomical signals are often extremely regular in their repetitiveness. They tend to stay in tune for a long time, and that gives rise to very strong and narrow peaks in the frequency domain.
There is interesting physics behind the fact that the astronomical signals are so regular. The first is the remarkable fact that the orbits of the planets happen to be nearly perfect ellipses, as mentioned earlier. This arises because the force of gravity is nearly a perfect 1/r2 force. It didn’t have to be this way. If the force of gravity were 1/r, or 1/Ãr, or 1/r3, we would not have closed orbits. In fact, the only other force law that gives a closed orbit is the linear spring law, F = –kr. (See L. D. Landau and E. M. Lifshitz, Mechanics, 3rd edition, p. 32.) But because gravity varies with the inverse square of the separation, the orbits repeat. If friction were present (and it is for really small particles; see Section 7.2), then the orbits would not close. General relativity theory is also a slight departure from the inverse square law, and a consequence of this is that the orbits of the planets do not completely close. One consequence is the "advance of the perihelion of Mercury." When astronomers measure this, they are studying the departure from the Newtonian inverse-square law. Perturbations from the other planets also cause departures from pure single-frequency periodicity, for the same reason. Although they are individually inverse-square, each planet’s contribution to the force comes from a different direction in space than that of the Sun, so when added to the Sun’s gravity, the net resulting force is not inverse square.
The most natural way to do spectral analysis of data is to try to fit it to a mathematical function containing sine waves. For example, if we have data points yk, each having an age tk then we could try to find the best parameters a0, ak, fk, and fk, such that we minimize the difference between the real data and the function:
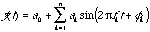
is minimized. (For an illustration of this processes, you can look ahead to our description of eccentricity in Section 2.2.2; in particular, Figure 2-7 on page * shows an orbital function called eccentricity closely approximated by the sum of three sine waves.) Many computer programs have been written for just this minimization process. (In the Matlab™ language, for example, the program is called fmins.m.) This approach is excellent, in principle; it is closely related to a method we will describe (Section 3.7) as the "Maximum Likelihood Method." Its main disadvantage is that it is very time consuming. A much faster method is to use the Fourier transform, for which very rapid methods of computation have been devised. But if part of the signal is periodic, and part is background, and if the time scale is uncertain, then performing a Fourier transform is often not the optimum approach. The discipline called spectral analysis has developed largely to determine the best approach to analyzing a periodic signal in the presence of background and uncertainty. The choice of technique to use depends on the nature of the signal (is it broad? a sine wave? a square wave?), the nature of the noise (Gaussian? broad or narrow band?), the accuracy of the data (error in time scale?), and the nature of the variable you want to measure (amplitude of the periodic component? frequency? phase? spectral shape?). Not only is such optimization important for science, but it can be extremely important in a competitive industry such as communications. The result is that the field of spectral analysis has become very sophisticated, and very arcane. Sometimes it feels too arcane – so full of traps, and so difficult to master, that otherwise excellent scientists just try to avoid it.
To make the optimum choice of spectral analysis technique requires a detailed understanding of the background, i.e. the part of the signal that we don’t want to study. But we usually don’t have that. The result is that there is no "correct" way to do the analysis, only ways that have different advantages and disadvantages, and different traps. The field of paleoclimate has been dominated for a long time by the use of the "Blackman-Tukey method," presented in detail in the classic 1958 book The measurement of power spectra . It is also reportedly the method that Tukey himself suggested be used for paleoclimate work. It is, in fact, particularly well suited for data with an uncertain time scale, as has been the case for much paleoclimate data.
We’ll give a simple example of spectral analysis here, while leaving the details to a later chapter. In an Antarctic ice core from Vostok, the relative fraction of the hydrogen isotope deuterium was measured as a function of depth. Using a model for the ice flow, this could be plotted as a function of time. The data were part of the basis for Figure 1-5. We show these data covering the entire period 0 to 420 kyr, in Figure 1-8.
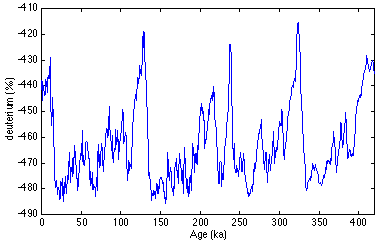
There appears to be a periodicity of approximately 100 kyr. This is evident in the spectral power plot shown in Figure 1-9. The plot was made using the periodogram method of Section 3.2.4.
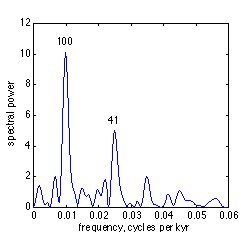
Figure 1-9 Spectrum of Vostok deuterium
From this plot, we see that in addition to the 100 kyr cycle (the peak near the frequency f = 0.01 cycles/ky), there is another prominent peak near 0.024 cycles/kyr. This is identified with an orbital parameter called obliquity, which is described in Section 2.2.4. It is not evident in the time domain because the eye is distracted by the strong 100 kyr cycle.
Our real purpose in showing the spectra here is to demonstrate how phenomena that are well hidden in the time domain, can stand out in the frequency domain. And it works both ways. The "sudden terminations" in the time plot are the nearly vertical lines that appear at the end of each glaciation. There is no evidence for these in the spectral plot. Such sharp changes require a conspiracy of a large number of small components at many different frequencies. These small contributions are well-hidden in the frequency domain. A comprehensive analysis of data requires analysis in both the time and frequency domains. Often it is necessary to do both, by breaking the data into segments of different time intervals, and doing the spectral analysis on each segment. This is important when the dominant cycles change with time, as they often do in paleoclimate data.