ABSTRACT: Narrow spectral features in ocean sediment records offer strong evidence that the cycles of glaciation were driven by astronomical forces. Two million years ago the cycles match the 41 k.y. period of the Earth's obliquity. This supports the Croll/Milankovitch theory, which attributes the cycles to variations in insolation. But for the last million years, the spectrum is dominated by a single 100 k.y. feature, and is a poor match to the predictions of insolation models. The spectrum can be accounted for by a theory which derives the cycles of glaciation from variations in the inclination of the Earth's orbital plane.

Nearly as soon as the ice ages were discovered, their origin was attributed to astronomical causes. In the late 1800s, James Croll assumed that the ice ages were driven by changes in insolation (solar heating) brought about by variations in the Earth's orbit and spin axis (1, 2). According to Croll, and to Milankovitch after him (3, 4), the main orbital parameters that affect insolation and its distribution are the Earth's orbital eccentricity, obliquity (tilt of the Earth's poles towards the sun), and precession (lag between equinox and perihelion). However, it was not until 1970 that Broecker and van Donk (5) established that glaciation in the late Pleistocene was truly periodic, and dominated by a 100 k.y. cycle. This period was soon identified with the quasi-periodic 100 k.y. cycle of the Earth's eccentricity. (We will offer evidence that this identification was premature.) In addition another strong cycle was discovered with a 41 k.y. period that matched the cycle of changes in the Earth's obliquity (8). This 41 k.y. cycle appears to have dominated glacial changes from 1.5 to 2.5 Ma (6). The 100 k.y. cycle has dominated from the present back to 1 Ma.

Much of the best data for paleoclimate studies comes from ocean sediments, in which proxies for climate, preserved in fossils, are measured as a function of depth. The oxygen isotope ratio, d¹⁸O, is believed to reflect the amount of the Earth's water frozen in ice, and thus is a measure of the Earth's global ice volume. To turn a record of d¹⁸O vs. depth into a record vs. time, the sedimentation rate must be estimated. This is often done with a process called tuning, in which the instantaneous sedimentation rate is deduced by matching cycles in d¹⁸O to calculated perturbations in the Earth's orbit. Parameterized sedimentation rates are adjusted to bring the observed proxy variations into consonance with the predictions of the model. This approach is potentially circular if the results are used to validate the climate model used to tune the record. Neeman (7) has demonstrated with Monte-Carlo tests that, given enough parameters, tuning procedures can successfully match data to an incorrect model, resulting in an inaccurate time scale as well as in a false validation of the model. Therefore, for the present work, we emphasize the use of time scales that are untuned, and which assume constant sedimentation with average rates constrained by radiometrically-measured control points.

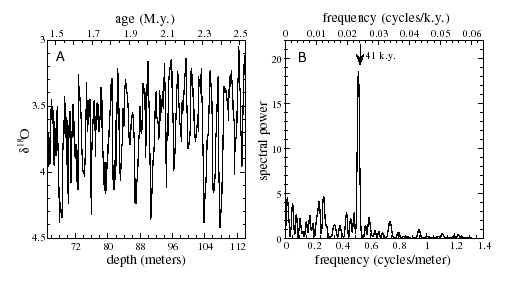
A strong case for astronomical forcing of glacial cycles comes from analysis of d¹⁸O data for the age interval 1.5 to 2.5 Ma from Deep Sea Drilling Project Site 607, located on the west flank of the Mid-Atlantic Ridge. For a full description of the stratigraphy, dating, and magnetic correlation, see Ruddiman et al.(8) and Raymo et al.(9). In their spectral analysis of the d¹⁸O data for the time interval 1.60 to 2.75 Ma, Ruddiman et al. (10) found a 41 k.y. peak with a full-width at half-maximum df/f of 12%. This is close to the width that would be obtained for a pure sine wave, using the low resolution spectral method that was employed (Blackman-Tukey (11) with 1/3 lags(12)). However, the time scale of this record had been tuned to obliquity, so it was conceivable that the relatively narrow width was an artifact of tuning.

The d¹⁸O data vs. depth is shown in Fig. 1A. To make an analysis that does not depend on tuning, we calculated the spectral power as a function of cycles per meter, using a method (13) that has about three times better frequency resolution than the method used by Ruddiman et al. The resulting spectrum is shown in Fig. 1B. It has one strong peak near 0.52 cycles/meter, with statistical significance greater than 99.9% (14). To place a time scale on the data, we assumed the same average sedimentation rate (15) used by Raymo et al. for this interval: 45.6 meters per million years. With this sedimentation rate, the peak in Fig 1B appears near the 41 k.y. period of obliquity.

Fig. 1 (A) Oxygen isotope data d¹⁸O in parts per thousand, and (B) spectral power, for Deep Sea Drilling Program Site 607, for the interval 1.5 to 2.5 Ma. The time scale assumes constant sedimentation rate.

The narrow width of this peak is the salient feature for the present discussion. The peak has a full-width at half-maximum of df/f = 3.7%. This is the same width that we obtain when we perform the same analysis on a pure 41 k.y. sine wave (or on any other perfectly periodic function, e.g. triangular, whose fundamental component is at 41 k.y.) for the same one million year duration (16). The fractional width of a periodic signal is independent of the assumed sedimentation rate, but depends solely on the number of cycles in the interval (17). The presence of a narrow peak in untuned data requires two phenomena: the existence of a nearly constant sedimentation rate, and the presence of a truly periodic signal.

The narrow width has important implications for climate models. In any climate model that depends on free oscillation, the width will be significantly broadened if substantial energy loss (friction) is present, or if the mode of oscillation is not isolated from other modes. For this reason, free oscillation climate models generally predict broad spectral peaks. Likewise, climate models based on relaxation oscillators usually have broad peaks. Relaxation oscillators tend to lose their phase stability (and their narrow spectral peaks) unless the energy exchange mechanisms are exceptionally constant over many cycles, a condition not expected to be met in the geophysics of climate. In contrast, a climate model that depends on forced oscillations has a spectrum that reflects the spectrum of the driving force, so that regardless of losses, narrow spectral features in the force will also appear in the response (18). The only natural driving forces in physics that have narrow spectra tend to be astronomical and quantum-mechanical, since friction is often negligible both in space and in atoms. (This is why the motions of the earth, moon, and planets provided the original calendars; and it is why quantum-mechanical devices provide the most accurate clocks.) Since we have no plausible way to relate the phase stability of the glacial cycles to quantum mechanics, we conclude that the oscillation is driven by an astronomical source. This is a general argument for the astronomical origin of the 41 k.y. cycle that does not depend on the details of any specific astronomical theory, e.g. the Croll/Milankovitch insolation model, or even on the frequency match between this cycle and the obliquity cycle.

Similar evidence for the astronomical origin of the 100 k.y. glacial cycle can be found in d¹⁸O data from Ocean Drilling Program Site 659, located in the Atlantic Ocean off Northwest Africa, near 18^o N and 21^o W (19, 20). The untuned d¹⁸O data for the age interval 0 to 900 ka is shown in Fig. 2A. The time axis was derived by taking the age of Tiedeman et al. (20) for the maximum depth and assuming constant sedimentation. The spectrum is shown in Fig. 2B. A strong narrow peak appears near f = 0.01 cycles/k.y. (100 k.y. period). The full-width at half-maximum of the peak is df/f = 9.8%, indistinguishable from the width one would obtain for a sine wave (16). It is highly unlikely that a single narrow peak would appear in the untuned data unless the sedimentation rate were relatively constant and there was a driving force with a strong single period. We conclude that the 100 k.y. cycle is astronomically driven.

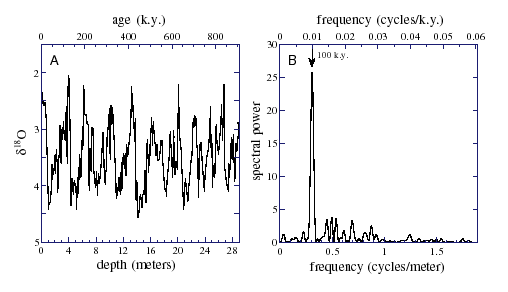
Fig. 2. (A) Oxygen isotope data d¹⁸O in parts per thousand, and (B) spectral power, for Ocean Drilling Project Site 659, for the interval 0 to 900 ka. The time scale assumes constant sedimentation rate.

To make a more comprehensive study of the 100 k.y. cycle, and to compare it with theory, we examined oxygen isotope records for cores at the following Deep Sea Drilling Project and Ocean Drilling Program sites located in the Atlantic, Pacific, and Indian Oceans: Site 552 (21), Site 607 (8, 9), Site 659 (19, 20), Site 664 (22), Site 677 (23, 24), Site 806 (25, 26), Site 849(27), and the Specmap stack (28). Site 806 has been shown to have a nearly constant sedimentation rate for the interval 0 to 840 ka (29). A narrow peak in the untuned data, evidence for nearly constant sedimentation, was also found in the spectra for Site 664 for the interval 0 to 600 ka.

In order to facilitate comparisons among the sites, we chose a common time interval covered by all the d¹⁸O data sets: 0 to 600 ka. In column A of Fig. 3 we show the spectra for this period expected from three climate models: a linear eccentricity model, a nonlinear ice model which derives its quasi-100 k.y. cycle from the envelope of the precession parameter (30), and an orbital inclination model (31, 32, 33). The frequency scale has been expanded to facilitate comparisons of the peak shape and structure. The orbital spectra were calculated using the results of Quinn et al.(34). The orbital inclination was transformed to the invariant plane as described by Muller and MacDonald (33); the values for the last three million years have been posted on the World Wide Web at www-muller.lbl.gov. The insolation-based models have spectral fingerprints with three peaks near 0.0025, 0.008, and 0.0105 cycles/k.y., corresponding to periods of 400, 125, and 95 k.y. The fingerprint of the inclination model has a single prominent peak near frequency 0.01 cycles/k.y., corresponding to a period of 100 k.y.

The spectra of the d¹⁸O data are plotted in the remaining columns of Fig. 3. Column B contains the spectra for the sites at which there was evidence (as discussed above) that the sedimentation rate was nearly constant: Sites 659, 664, and 806. Column C contains the data for which the sedimentation rate showed evidence of variability during the 0 to 600 k.y. interval, but for which a minimally-tuned time scale was available: Sites 552, 607, and Specmap. (By minimally-tuned, we mean that the sedimentation rate was tuned, at most, to obliquity and precession, but that there was no 100 k.y. cycle in the target curve. Such tuning can artificially enhance and narrow the 41 k.y. and 23 k.y. peaks; if done badly, it could destroy the 100 k.y. peak, but it is unlikely to artificially narrow the 100 k.y. peak.) Column D has spectra of data that showed strong evidence for sedimentation rate variability and for which the only time scale that had been published was tuned to a climate model that included eccentricity.

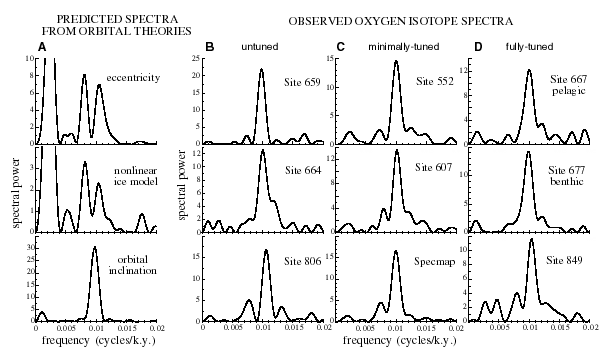
Fig. 3. Spectra of orbital models and of the d¹⁸O data (a proxy for global ic) for the interval 0 to 600 ka. The frequency scale has been expanded to facilitate comparison of peak shapes near 0.01 cycles/k.y. (period 100 k.y.). Column (A) shows spectra of three possible drivers for the glacial data: a linear eccentricity model, a nonlinear ice model that derives the 100 k.y. signal from the envelope of precession parameter, and an orbital inclination model. The next three columns show the spectral power of d¹⁸O data. Column (B) shows data with untuned time scales. Column (C) shows data with minimally tuned time scales (tuned to periods of 41 and 23 k.y.). Column (D) shows data with fully-tuned time scales, that is, the target climate model included an explicit 100 k.y. eccentricity cycle. All the data show a similar pattern: a single narrow peak near frequency f = 0.01 cycles/k.y. (period 100 k.y.), in good agreement with the orbital inclination theory, and in disagreement with the complex spectra predicted by the eccentricity- and precession-based theories.

There is a remarkably consistent pattern in the d¹⁸O spectral fingerprints in Fig. 3. All show a single narrow peak near frequency 0.01 cycles/k.y. (period 100 k.y.), similar to the spectrum of the orbital inclination model. None of the spectra show the multiple peak structure expected from the insolation theories. Even the fully-tuned data sets in column D, which are suspect because they were tuned to eccentricity, are a better match to the inclination model than to the eccentricity or nonlinear ice models. This evidence suggests that orbital inclination is the primary driving force for the global ice proxy d¹⁸O during the last million years, although we cannot rule out a small contribution by eccentricity or precession. Several of the spectra show small peaks near f = 0.008 (period 125 k.y.), characteristic of the insolation models, but these peaks have low statistical significance and could be noise fluctuations. None of the d¹⁸O data show either the expected doublet (125 and 95 kyr periods) or the strong peak near f = 0.0025 (400 k.y. period) present in the insolation models. It has been argued that the 400 k.y. cycle can be suppressed by geologic response (35). However, there are at least two other climate records, unrelated to glacial volume, that show the complete triplet structure expected from eccentricity (400, 125, 95 k.y. peaks): the coarse component (large foraminifera fraction) of sediment at Site 806 (29), and Triassic lake-bed depth ranks (36). These examples show that the 400 k.y. peak is not necessarily suppressed by the Earth response, and so its absence in the d¹⁸O record must be considered additional evidence against eccentricity or precession as a driving force for variations in global ice volume. These examples also show that eccentricity and precession do affect other aspects of climate. At Site 806, signals from inclination and eccentricity were found to be present simultaneously (29). However, the eccentricity signal was in a proxy thought to be sensitive to local climate (the coarse fraction of the sediment), whereas the inclination signal was in the proxy for global ice fraction (d¹⁸O).

The shift of the dominant glacial cycle from 41 to 100 k.y., which took place about a million years ago, can be understood if the mechanism that links orbital inclination to climate is the accretion of extraterrestrial dust. In 1994, Muller (31) postulated that the sudden onset of the 100 k.y. cycle might have been be caused by an increase in the amount of interplanetary dust or meteoroids at that time. An abrupt increase in accreted dust at about 1 Ma was subsequently reported by Farley in a study of ³He in sediment (37). When accretion was low, the dominant driving force for glaciation was obliquity, perhaps through a Croll/Milankovitch insolation mechanism. After the dust increase, the 41 k.y. obliquity cycle continued, but obscured under the stronger dust-driven inclination cycles. The strongest cycle predicted by many insolation models has period 23 k.y. Yet this cycle is weak in all the d¹⁸O records we have studied. This cycle would be naturally suppressed, even when insolation is the dominant driving force of glaciation, if ice volume is not particularly sensitive to the north/south land mass asymmetry on the Earth. Previous insolation mechanisms could not invoke this suppression because they required a strong precession contribution in order to account for the 100 k.y. cycle, a cycle we attribute instead to inclination.

One of the predictions of the accretion theory was that 100 k.y. cycles in dust or meteoric material could be found in sedimentary material or glacial ice, although an initial search failed to achieve sufficient sensitivity (31). To test this prediction, Farley searched for cycles of ³He in sediment, and found the predicted 100 k.y. cycle, with the times of high accretion roughly coincident with the interglacials; however Farley's results are disputed by Marcantonio (38). It is possible that the bulk of the dust would have a different phase. The ³He measurements are sensitive primarily to dust particles with a diameter of about 7 xm, whereas most of the accretion comes from particles larger than 50 xm (39). The orbits of the dust particles depend strongly on size, since their path to the Earth is determined primarily by the Poynting-Robertson effect (viscosity from sunlight), and while enroute to the Earth their orbits are perturbed by Jupiter and the other planets.

A narrow ring of dust around the sun was detected by the Infrared Astronomical Satellite (40, 41). This ring is within 1/2 degree of the dust band assumed in the accretion model. According to Dermott et al. (42), this dust is continually replenished by collisions among the members of the Themis and Koronis asteroid families. Kortenkamp et al. (43) have calculated that most of the extraterrestrial accretion on the Earth comes from this narrow solar ring. The event a million years ago that increased the rate of injection of interplanetary dust could have been a particularly disruptive collision in the Themis or Koronis families. According to Kortenkamp et al. (43), the cyclicity of accretion observed by Farley is a necessary consequence of the known dust orbits combined with orbital calculations.

Although the spectra of d¹⁸O imply that the global ice volume is forced predominately by orbital inclination and obliquity, other aspects of climate seem to be driven by eccentricity or precession. Thus it appears that glacial cycles are not completely synonymous with climate cycles. It will be a challenge to future geophysical models to account for the dichotomy.

References and notes 

1. J. Croll, Phil. Mag. 33, 426-445 (1867).

2. J. Croll, Climate and time (Appleton & Co., New York, 1875).

3. M. Milankovitch, Théorie Mathématique des Phénomènes Produits par la Radiation Solaire (Gauthier-Villars, Paris, 1920).

4. M. Milankovitch, Canon of Insolation and the Ice-Age Problem, Royal Serbian Acad. Sp. Pub. 132 (Royal Serbian Academy, Belgrade, Yugoslavia, 1941).

5. W. S. Broecker, J. van Donk, Rev. Geophys. Space Phys. 8, 169-197 (1970).

6. J. Hays, J. Imbrie, N. Shackleton, Science 194, 1121-1132 (1976).

7. B. U. Neeman, "Orbital Tuning of Paleoclimatic Records: a Reassessment" LBNL-39572 (Lawrence Berkeley National Laboratory Report LBNL-39572, 1993).

8. W. F. Ruddiman, M. E. Raymo, D. G. Martijnson, B. M. Clement, J. Backman, Plaeoceanography 4, 353-412 (1989).

9. M. E. Raymo, W. F. Ruddiman, J. Backman, B. M. Clement, D. G. Martinson, Paleoceanography 4, 413-446 (1989).

10. W. F. Ruddiman, M. Raymo, A. McIntyre, Earth and Planetary Science Letters 80, 117-129 (1986).

11. R. B. Blackman, J. W. Tukey, The measurement of power spectra (Dover, New York, 1958).

12. The Blackman-Tukey method obtains the spectral power by first forming the autocorrelation function of the data, and then performing a Fourier transform. If only a partial autocorrelation is performed, e.g. if the maximum delay is only 1/3 of the time interval of the data set, then we say the "lag" is 1/3. The spectral peak in the lagged analysis is broadened by a factor equal to 1/lag.

13. Spectral power is computed by interpolating the data to equally-spaced points, removing the average (but not the trend), using a boxcar window (i.e. taking all points equally weighted), and then taking the square of the Fourier transform. The spectrum is normalized to unit mean. The data presented here have also been examined with other spectral methods (e.g. Blackman-Tukey with various lags, and Lomb-Spergel) and other windows (e.g. Hanning and Parzen). The conclusions are robust to all data methods, excluding those that significantly degrade the resolution and therefore could not resolve the narrow features from which we draw our conclusions.

14. The background spectral power in the vicinity of this peak is 1.5; the height of the peak is 18.5; this means that the peak is significant at the level of exp(-18.5/.1.5) = 4 x10^-6. Since there are approximately 50 independent frequencies in the plot, the confidence level for this peak is CL = 1-(50)x(4x10^-6) = 99.98%.

15. The age of 1.5 Ma corresponds to an adjusted depth of 66.83 meters, and the age of 2.5 Ma corresponds to an adjusted depth of 112.40 meters. These give an average sedimentation rate of 45.6 meters/Myr.

16. The full-width at half maximum Æf of the spectral peak that results from calculating the spectral power of a pure sine wave (or any other perfectly periodic signal) of duration T, is df = 0.886/T. This width could be made larger by applying a window to the data (e.g. a Hanning window) that deemphasizes data at the beginning and end of the interval; the width can be made smaller by applying a window that emphasizes the two ends of the interval. In this paper we weight all data equally; this is sometimes called a flat or a boxcar window. For a 600 kyr interval, the width is Æf = 0.886/600 = 1.5 x10^-3 cycles/kyr; the separation of the components of the 95/125 eccentricity doublet is significantly larger: 2.5 x10^-3 cycles/kyr. For a 900 kyr interval, the width is Æf = 9.8 x10^-4 cycles/kyr.

17. The frequency of oscillation is f = 1/P, where P is the period; the full-width at half-maximum is df = 0.886/T, where T is the duration of the interval. Therefore the fractional width is df/f = (0.886/T)P = 0.886/N, where N = T/P is the number of cycles in the interval T.

18. The response may have a different phase than the driving force, but it has the same frequency, even if several resonances are present. For a simple introduction to some of the properties of forced and free oscillations, see J. B. Marion and S. T. Thornton, "Classical Dynamics of Particles and Systems," Harcourt Brace Jovanovich, publishers (1988).

19. M. Sarnthein, R. Tiedemann, Proc. Ocean Drilling Program, Sci. Results 108, 167 (1989).

20. R. Tiedemann, M. Sarnthein, N. J. Shackleton, Paleoceanography 9, 619-638 (1994).

21. N. J. Shackleton, M. A. Hall, in Initial Reports of the Deep Sea Drilling Project . (U.S. Government Printing Office, Washington, D.C., 1984), vol. 81, pp. 599-609.

22. M. E. Raymo, D. W. Oppo, W. Curry, Paleoceanography , in revision (1997).

23. N. J. Shackleton, M. A. Hall, in Proceedings of the Ocean Drilling Program, Scientific Results . (Ocean Drilling Program, College Station, Texas, 1989), vol. 111, pp. 295-316.

24. J. J. Shackleton, A. L. Berger, W. R. Peltier, Transactions of the Royal Society of Edinburgh, Earth Sciences 81, 251-261 (1990).

25. W. H. Berger, T. Bickert, H. Schmidt, G. Wefer, in Proceedings of the Ocean Drilling Program, Scientific Results . (Ocean Drilling Program, College Station, Texas, 1993), vol. 130, pp. 381-395.

26. W. H. Berger, M. K. Yasuda, T. Bickert, G. Wefer, T. Takayama, Geology 22, 463-467 (1994).

27. A. C. Mix, et al., Proceedings of the Ocean Drilling Program, Scientific Results 138, 371-412 (1991).

28. J. Imbrie, et al., in Milankovitch and Climate Part 1 A. Berger, etal., Eds. (D. Riedel, Dordrecht, 1984) pp. 269-305.

29. R. A. Muller, G. J. MacDonald, Geology 25, 3-6 (1997).

30. J. Imbrie, J. Z. Imbrie, Science 207, 943-952 (1980).

31. R. A. Muller, "Glacial cycles and extraterrestrial accretion" LBL-35665 (Lawrence Berkeley Laboratory Report LBL-35665, 1994).

32. R. A. Muller, G. J. MacDonald, Nature 377, 107-108 (1995).

33. R. A. Muller, G. J. MacDonald, Spectrum of 100 kyr Glacial Cycle: Orbital Inclination, Not Eccentricity, Conference on Carbon Dioxide and Climate, Irvine California (Nat. Acad. Sci. U.S.A., in press 1997).

34. T. R. Quinn, S. Tremaine, M. Duncan, Astronomical Journal 101, 2287-2305 (1991).

35. J. Imbrie, et al., Paleoceanography 8, 699-735 (1993).

36. P. E. Olsen, D. V. Kent, Palaeogeography, Palaeoclimatology, Palaeoecology 122, 1-26 (1996).

37. K. Farley, Nature 378, 153-156 (1995).

38. K. Farley, D. B. Patterson, Nature 378, 600-603 (1995). However, F. Marcantonio has found no evidence for such cycles (put ref here).

39. K. A. Farley, S. G. Love, D. B. Patterson, Geochimica et Cosmochimica Acta (submitted, 1997).

40. M. Sykes, Astrophys. J. 334, L55-L58. (1988).

41. M. V. Sykes, et al., in Asteroids II T. G. R. Binzel, M Matthews, Ed. (Univ Arizona Press, Tucson, 1989) pp. 336-367.

42. S. F. Dermott, P. D. Nicholson, J. A. Burns, J. R. Houck, Nature 312, 505-509 (1984).

43. S. J. Kortenkamp, S. F. Dermott, J. C. Liou, in Physics, Chemistry, and Dynamics of Interplanetary Dust B. Gustafson, M. Hanner, Eds. (1996), vol. 104, pp. 167-170.

ACKNOWLEDGMENTS

We thank W. Alvarez and the Renaissance Geology Group for many stimulating discussions. We thank M. Raymo, W. Berger, M. Yasuda, P. Olsen, and S. Clemens for providing data in digital form. Additional data were obtained over the World Wide Web from the site maintained by NOAA at www.ngdc.noaa.gov. This work was supported, in part, by the Department of Energy (under contract no. DE-AC03-7bSF00098) and by the Ann and Gordon Getty Foundation.